Define Mealy and Moore Machine

RGPV 2010

Q. Formally define the following (with example)-

1. Mealy machine

2. Moore machine

1. Mealy machine: Mealy machine is a six tuple machine.M = (Q, Σ, △, δ, λ, q0)

1. Q is finite set of states.
2. Σ is the input alphabet.
3. △ is the output alphabet.
4. δ is transition function which maps Q×∑ → Q.
5. ‘λ’ is the output function which maps Q×∑→ △.
6. q0 is the initial state.

Transition table for Mealy machine

Transition diagram for Mealy machine

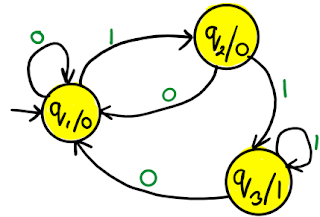
1. Moore machine: Moore machine is a six tuple machine.M = (Q, Σ, △, δ, λ, q0)

1. Q is finite set of states.
2. Σ is the input alphabet.
3. △ is the output alphabet.
4. δ is transition function which maps Q×∑ → Q.
5. ‘λ’ is the output function which maps Q → △.
6. q0 is the initial state.

Transition table for Moore machine

Transition diagram for Moore machine

Mealy machine vs Moore machine

Mealy machine	Moore machine
Output depends on present state as well as present input.	Output depends on the present state.
If input changes, output also changes	If input changes, output does not changes.
Compare to Moore less number of states are required. Because states do not depends on output.	Compare to Mealy more number of states are required. Because states depends on number of output.
Difficult to develop. Difficulty due to input affects output.	Easy to develop.
Output is placed on transition arrow.	Output is placed with state.

---

Practice problems: