NFA with ∈ moves is exactly same as NFA without ∈ moves.
But differece exist in the transition function δ. δ must include information about ∈ transitions.
NFA with ∈-Moves has 6 tuples (Q, Σ, δ, q0, F).
Where,
- Q = finite set of states.
- Σ = finite set input symbols.
- δ = transition function that maps Q × (Σ ∪{∈}) to 2Q.
- q0 = initial state.
- F = set of final states.
The non-deterministic finite automaton can be extended to include the transitions on null/empty input ∈.
For example,

In this NFA with epsilon,
- It accept an input string ‘aabc’.
- Or string as number of a’s followed by number of b’s followed by number of c’s.
- The string ‘aabc’ is accepted by the NFA by following the path with labels a, a, ∈, b, ∈, c.
Transition table for above NFA.
∈-closure
∈-closure of a state q is a set of states following by all transitions of q that are labeled as ∈.
- ∈-closure (q0) = (q0, q1, q2)
- ∈-closure (q1) = (q1, q2)
- ∈-closure (q2) = (q2)
NFA with ∈ to NFA without ∈

Transition diagram
Transition table NFA with ∈
First find out ∈ closure:∈-closure
- (q0) = (q0, q1, q2)
- ∈-closure (q1) = (q1, q2)
- ∈-closure (q2) = (q2)
Transition table NFA without ∈
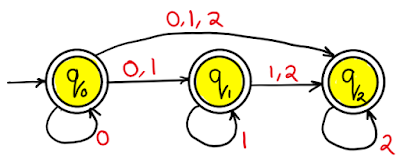
Transition diagram
Reference:
- Introduction to the Theory of Computation” by Michael Sipser.


